Son réseau est cubique à faces centréesa ) Nombre d'ions dans une maille
3 ) Cas des structures cubiques
Un cristal est un assemblage infini et régulier d'atomes. Cette régularité s'explique par l'existence des réseaux et des mailles.
Un réseau est un ensemble de points (ou nœuds) dans l'espace, donc en trois dimensions. Un réseau présente la propriété de retrouver le même environnement lorsqu'on le translate dans l'espace selon certains vecteurs. Il y a donc une périodicité spatiale à l'origine de la régularité du cristal. Tous les points d'un réseau représentent un même motif. Ce même motif est donc le plus petit constituant qui, s'il est translaté, permet de reconstituer l'intégralité du réseau. Il contient donc au moins un exemplaire de chacun des ions du cristal. Le motif n'est pas le même pour tous les cristaux. Chaque cristal ionique étant issu d'un échange d'ions entre deux atomes qui doivent être différents, un motif contient au minimum deux ions différents, comme c'est le cas par exemple pour un cristal de sel (NaCl) : le motif est constitué d'un ion chlore (Cl-) et d'un ion sodium (Na+) (voir image).
La notion de réseau est née en géologie, avant que l'on ne connaisse les atomes ; Haüy et Bravais, en étudiant la symétrie extérieure de certains cristaux et notamment le fait que le clivage se fasse selon certains plans, en déduisirent que "l'organisation interne" de la matière devait avoir les mêmes symétries. S'appliquant à l'origine aux cristaux minéraux, ceci s'applique également aux cristaux ioniques.
Un réseau peut se limiter à une portion de réseau ayant les mêmes symétries que le réseau entier. Cette portion est donc un prisme constitué de plusieurs nœuds. Le réseau est un empilement de ces portions. Par convention, quand on parle d'un cristal, le terme de réseau désigne non pas l'ensemble du réseau du cristal mais cette portion de réseau qui est la plus petite partie dont est constitué exclusivement le cristal. En effet, elle suffit pour caractériser le réseau de l'ensemble du cristal.
Chaque réseau possède différents paramètres. Tout d'abord il y a trois dimensions notées a b c et trois angles notés a b g. Ces paramètres permettent de placer un réseau dans l'un des sept systèmes cristallins. En plus des nœuds à ses sommets, un réseau peut avoir des nœuds placés en son centre ou au centre des faces. Ce paramètre identifie un réseau à l'un des quatorze réseaux de Bravais.
Pour représenter un cristal ionique et son organisation spatiale, on dessine sa maille. La notion de maille est très semblable à celle de réseau. La différence réside dans le fait qu'une maille fait apparaître non pas l'emplacement des motifs mais des ions eux-mêmes. La maille d'un cristal est la plus petite partie du cristal qui caractérise l'organisation spatiale des ions dans le cristal, on parle également de maille élémentaire. Le cristal est un empilement de représentations de sa maille. Comme pour les réseaux, les mailles possèdent les trois paramètres de dimensions a b c et les trois paramètres d'angle a b g (voir Les sept systèmes cristallins pour plus de détails sur ces paramètres).
Prenons le cas du NaCl :
Son réseau est cubique à faces centrées
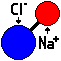Son motif est composé d'un ion Na+ et d'un ion Cl-
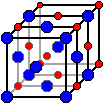Décomposition en deux sous-réseaux cubiques à faces centrées
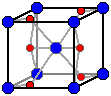
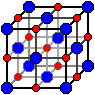Maille du cristal NaCl, qualifiée également de cubique à faces centrées
Quand on donne la maille d'un cristal, on représente par convention la maille avec les
cations et non les anions aux sommets. Mais la maille d'un cristal peut très bien être
représentée avec les anions à ses sommets.
Exemple de la fluorite CaF2 : les sommets de la maille de gauche sont des
cations (ici Ca2+) ceux de la maille de droites des anions (ici F-).
Toutes les mailles ne se construisent pas de la même façon, néanmoins, il existe un certain nombre de mailles caractéristiques (appelées également structures) qui peuvent s'appliquer à plusieurs cristaux. Ainsi, pour des structures binaires, en calculant le rapport du rayon de l'anion sur le rayon du cation, on peut déterminer la structure d'un cristal.
Pour les structures de type AB
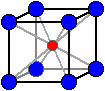
| Si rA/rB > 0,7
la structure est souvent du type du chlorure de césium CsCl Représentants : CsCl, CsBr, CsI |
|
| Si 0,7 >rA/rB > 0,4
la structure est souvent du type du chlorure de sodium NaCl Représentants : KF, CaO, NaF, KCl, SrS, RbI, KBr, CaS, KI, MgO, LiF, NaCl, NaBr, MgS,NaI, LiCl, LiBr, LiI |
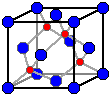
| Si 0,4 >rA/rB > 0,2
la structure est souvent du type de la blende ZnS Représentants : BeO, BeS, BeSe |
Pour les structures de type AB2
|
| Si rA/rB > 0,7
la structure est souvent du type de la fluorite CaF2 Représentants : BaF2, PbF2, SrF2, ThO2, CaF2, UO2, CeO2, CdF2, ZrF2, HfF2 |
| Si 0,7 >rA/rB > 0,4
la structure est souvent du type du rutile TiO2 Représentants : TeO2, MnF2, PbO2, FeF2, CoF2, ZnF2, NiF2, MgF2, SnO2, MoO2, WO2, TiO2, VO2, MnO2 |
L'image précédente montre bien que le cristal est formé de mailles identiques mises bouts à bouts. Ainsi, un ion peut appartenir à plusieurs mailles en même temps, de une seule à huit suivant sa position dans la maille. On peut ainsi déterminer le nombre d'ions d'une maille en fonction de leur taux d'appartenance à la maille :
Prenons par exemple la maille du NaCl :
ions Cl- : 8 aux sommets et 6 sur des faces,
soit 8x1/8 + 6x1/2 = 4 ions Cl- par maille
ions Na+ : 12 sur des arêtes et un au centre,
soit 12x1/4 + 1x1 = 4 ions Na+ par maille
On retrouve bien le même nombre d'ions Cl- et d'ions Na+
stœchiométrie 1:1).
Connaître le nombre d'ions présent dans une maille permet de déterminer
plusieurs propriétés de la maille.
On peut exprimer la masse d'une maille en fonction du nombre d'ions par
maille et de la masse molaire de chaque ion :
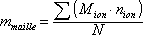
avec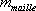 
la masse de la maille,
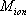la masse molaire des différents ions de la maille,
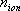la quantité des différents ions dans la maille
et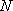 
le nombre d'Avogadro.
La masse des électrons étant négligeable face à la taille du noyau, on peut
considérer que la masse molaire d'un ion est égale à la masse molaire de
l'atome qui lui correspond.
Pour la maille de NaCl : 
.
On peut également calculer le volume d'une maille. En effet, Toutes les mailles sont des prismes. À partir des valeurs a b c qui correspondent aux longueurs des arêtes de la maille, on peut donc donner une formule générale du volume d'une maille : V = a b c. Pour une maille hexagonale, il faut légèrement modifier la formule car une maille est constituée de trois prismes égaux, on a alors V = 3 a b c. Pour certaines mailles, quand deux paramètres voire les trois (pour les mailles appartenant au système cubique par exemple) la formule peut-être simplifiée, ainsi pour une maille cubique on a V = a3.
Maintenant que l'on connaît le volume d'une maille et sa masse, il est facile de calculer sa masse volumique de formule générale m = m / V. Grâce à cette valeur, connaître la masse d'un cristal permet d'obtenir son volume et vice-versa en utilisant la relation précédente.
Une maille n'est pas totalement remplie par les ions, on voit qu'il y a
des espaces entre eux. La compacité d'une maille est le rapport entre le
volume occupé par les ions et le volume total de la maille. Cette valeur
est donc comprise entre 0 et 1. On peut calculer le volume occupé par les
ions à partir de leur nombre dans la maille et de leur rayon. Cela donne la
formule suivante :
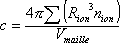où
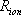est le rayon de l'ion,
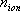le nombre d'ion et
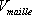le volume de la maille.
Pour pouvoir traiter des indices de Miller, il faut tout d'abord introduire la notion de plan nodal. Un plan nodal est l'ensemble des nœuds (dans le cas d'un cristal ionique il s'agit des ions) situés sur un plan de l'espace. Cette notion peut s'appliquer aux réseaux comme aux mailles, tous deux étant des portions de l'espace.
Pour définir un plan (notamment son orientation), on donne trois nombres
entiers mis entre parenthèses. Ces trois nombres sont appelés indices de
Miller et par convention notés h k l. On parle ainsi des plans
(100) (prononcer un-un-zéro), (110), etc… On définit pour chaque
réseau et pour chaque maille une base vectorielle qui leur est liée. Les
vecteurs de la base sont les arêtes du réseau (ou de la maille) de longueur
a b c et formant des angles entre eux de mesure a b
g. Pour le système cubique
la base est orthonormée. L'orientation d'un plan est alors décrite, comme en
mathématiques, par la donnée de son vecteur normal. Dans le cas d'un réseau
cubique, ce vecteur est perpendiculaire au plan. Dans le cas d'un réseau
quelconque, il n'est plus perpendiculaire au sens "angle droit", mais si on
déformait la maille pour la rendre cubique, alors il le deviendrait. Ce sont
les coordonnées de ce vecteur qui forment les indices de Miller. Lorsque des
coordonnées de vecteur sont négatives, on place une barre au-dessus de l'indice
de Miller correspondant : par exemple, le plan représenté par le vecteur
de composantes (-1,1,2) sera noté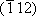 
.
Cependant, la barre au-dessus ne faisant pas partie des polices informatiques
standard, on l'écrit souvent (-112) (prononcer moins un-un-deux). Pour
des raisons géométriques évidentes, si l'on change le signe de chaque nombre
on obtient le même plan : (hkl) = (-h-k-l).
Voici quelques exemples d'indices de Miller et de leur plan
associé pour des systèmes cubiques.
La périodicité du cristal entraîne le fait qu'il existe une infinité de plans de mêmes indices parallèles entre eux. On appelle distance inter-reticulaire, notée dhkl, la distance qui sépare deux plans parallèles voisins.
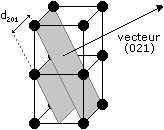
Ce schéma montre bien la distance inter-réticulaire ainsi que le vecteur
normal d'indice de Miller (201).
Sur le même principe que les plans nodaux, il existe également les rangées nodales. Une rangée nodale est une droite de l'espace passant par des nœuds du cristal. Une rangée nodale est définie de la même façon que le vecteur normal d'un plan. On utilise donc là aussi les indices de Miller cette fois les entiers sont mis entre crochets : [uvw]. On parle également de direction cristallographique pour désigner les indices [uvw].
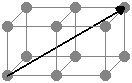
Voici un exemple de rangée nodale d'indice (-121)
Du fait qu'elles possèdent une base orthonormée (et elles sont les seules), on peut appliquer toutes les relations classiques de la géométrie et de la trigonométrie aux structures cubiques. On peut par exemple aisément calculer leur distance inter-réticulaire.
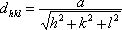où a est le paramètre de la maille (longueur de l'arête)
De plus du fait des symétries, on remarque qu'en permutant les indices et les signes on obtient le même plan. On parle alors de famille de plans notée {hkl}. Par exemple la famille {100} est composée des plans (100), (010), (001), (-100), (0-10), (00-1). De même il existe des familles de rangée notées <uvw> qui suivent le même principe.
Rappelons tout de même que ceci n'est valable que dans le cas d'un réseau ou d'une maille cubique.