
Dans l'ordre, un cercle, une ellipse, une parabole et une hyperbole
I - Les différentes formes d'orbites
Une orbite est la trajectoire d’un corps animé d’un mouvement périodique, autour d’au moins un corps central.
L'orbite d'un corps autour d'un autre corps peut être un cercle, une ellipse, une parabole ou une hyperbole. Ces quatre figures géométriques constituent l'ensemble des coniques car elles sont obtenues par l'intersection d'un cône de révolution avec un plan ne contenant pas le sommet du cône.




Dans l'ordre, un cercle, une
ellipse, une parabole et une hyperbole
On appelle e l'excentricité de la conique (et donc de l'orbite),
alors :
- si e = 0, l'orbite est un cercle
- si e <
1, l'orbite est une ellipse
- si e = 1, l'orbite est une parabole
-
si e > 1, l'orbite est une hyperbole
Notons que ceci n'est valable que si le corps en orbite est attiré par un seul corps. Dans le cas contraire, l'orbite sera sans cesse perturbée par des corps différents et la conique qu'elle suivra sera sans cesse modifiée.
L’orbite des planètes est régie par plusieurs paramètres, l’influence gravitationnelle du Soleil n’étant que l’un d’entre eux, quoique bien sûr, le plus puissant. On pense actuellement que l’orbite est constante, que la distance au soleil est maintenue par la force centrifuge qui écarte du soleil, que la rotation des planètes est constante.
Les planètes en orbite sont en effet capturées par le champ gravitationnel du Soleil, mais il y a plus en jeu que la gravité et le mouvement pour maintenir la distance qu’elles ont au Soleil. La vitesse orbitale est à peine assez grande pour créer une force centrifuge suffisamment puissante pour les garder à distance du Soleil. Les planètes ne dérivent pas vers le Soleil, en somme, à cause d’une force de répulsion générée dans les deux corps. Si la force gravitationnelle est constante, et attire en permanence un objet plus petit vers un plus gros, une force de répulsion est générée entre les objets, et ne devient assez puissante que lorsque la masse des deux objets est suffisante. Les objets très petits tels les comètes ou les météorites qui s’écrasent régulièrement sur le Soleil ou sur les planètes en orbite ne génèrent pas de force de répulsion suffisante pour contrecarrer la gravité, du fait de leur minuscule masse proportionnellement au Soleil ou aux planètes. Quand leur trajectoire les amène à proximité, elles sont prises dans l’attraction gravitationnelle.
Les planètes sont en orbite parce qu’elles sont attirées par autre chose encore que par le champ gravitationnel du Soleil, autre chose encore que par le compagnon noir du Soleil qui joue le rôle de second foyer de la douzième planète, et certainement autre chose encore que les autres planètes, quoique cela soit à moindre échelle. Pour ceux qui doutent qu’il existe des influences gravitationnelles hors du Système Solaire, agissant sur les planètes en orbite, nous mentionnerons les trajectoires elliptiques que suivent les planètes. Si les planètes n’étaient concernées que par le Soleil, ou entre elles, elles ne suivraient pas des trajectoires elliptiques. Les planètes suivent des orbites elliptiques pour la même raison que les comètes quittent le Système Solaire. Elles écoutent un autre appel. A savoir pourquoi cette voix et aucune autre appelle cette planète et pas une autre, la réponse tient dans la force de gravité. La gravité peut être très variable, en fonction de la masse (liée à la composition) et de la distance, et la force d’un corps sur un autre peut avoir peu d’effet sur d’autres corps.
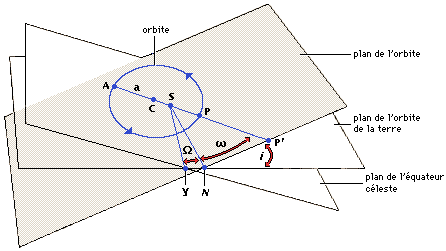
Six éléments caractérisent une orbite. Les deux premiers sont la dimension et l'élongation. La dimension d'une orbite est donnée par la distance du corps central au périastre (SP), et l'élongation par l'excentricité (e). Dans le cas d'une ellipse, l'excentricité correspond au rapport CS/CP, où S est le foyer et C le centre de l'ellipse. Pour les orbites elliptiques, e est supérieur à 0, mais inférieur à 1 ; pour les orbites circulaires, e est exactement égal à 0. Pour les orbites paraboliques, e est exactement égal à 1. Un corps en orbite hyperbolique effectue un seul passage près du corps central et s'échappe sur une trajectoire appelée orbite ouverte : le premier corps ne s'approchera plus du second astre.
Avant d'introduire les trois paramètres qui concernent l'orientation de l'orbite, il est nécessaire de définir les notions suivantes : pour les astres en orbite autour du Soleil, le plan de référence est le plan de l'orbite de la Terre, également appelé plan de l'écliptique ; l'équinoxe de printemps ou point vernal (U) matérialise l'intersection de l'équateur et de l'écliptique correspondant au passage du Soleil de l'hémisphère Sud à l'hémisphère Nord, au début du printemps boréal ; enfin, le nœud ascendant (N) est le point d'intersection entre l'orbite étudiée et le plan de référence franchi par le corps céleste lorsqu'il se dirige du sud vers le nord.
Ces éléments de référence servent donc de repère pour exprimer l'inclinaison (i), la longitude du nœud ascendant (W), et l'argument du périhélie (w) : l'inclinaison est l'angle entre le plan de l'orbite et le plan de référence ; la longitude du nœud ascendant est l'angle formé dans le plan de référence par la direction du nœud ascendant et celle du point vernal ; l'argument de périhélie est l'angle formé dans le plan de l'orbite par le nœud ascendant et la ligne reliant le périhélie (P) au centre de l'orbite (C). Le sixième élément orbital est temporel : c'est l'instant où l'astre franchit le périhélie.
La dimension de l'orbite s'exprime également par la longueur du demi-grand axe (AC, CP, ou a), qui est supérieure à la distance (SP), inférieure à la distance (AS), la différence (CS) étant égale au produit du demi-grand axe par l'excentricité :
CS = e(AC) = e(CP) = ea
Pour calculer la trajectoire de plusieurs corps dans un même système, il faut calculer les coordonnées successives de ces corps. Nous allons vous donner une méthode qui permet d'y parvenir.
Tout d'abord, il faut connaître la masse et les coordonnées de départ des différents corps.
Pour chaque corps, on calcule les composantes de la résultante des forces extérieures qui s'exercent sur lui (c'est-à-dire les forces d'attraction gravitationnelle de chacun des autres corps) grâce à la loi de la gravitation.
La deuxième loi de Newton nous dit que  , on en déduit les composantes de l'accélération.
, on en déduit les composantes de l'accélération.
Puis on calcule les composantes de la vitesse données par 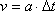
Enfin on trouve les nouvelles coordonnées données par 
L'équation finale est donc la suivante : 
Pour le calcul soit valable, il faut prendre l'intervalle de temps le plus petit possible. On peut de cette manière obtenir une bonne approximation de l'orbite d'un corps.
C'est cet algorithme appelé méthode de Verlet, qui est utilisé dans le logiciel de simulation d'orbite.