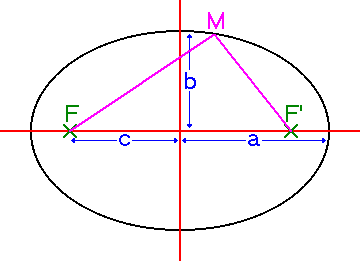
Soit deux points F et F'.
Une ellipse est l’ensemble des points M tels que MF + MF' soit une constante.
L’ellipse peut s’obtenir par intersection d’un cône par un plan de telle façon que le plan ne coupe pas la base, c’est pourquoi l’ellipse fait partie des coniques.
On appelle :
"a" le demi grand rayon
"b" le demi petit rayon
"c" la distance du centre l’ellipse aux foyers
"e" l'excentricité

Pour toute ellipse on a :
MF + MF' = 2a
a² = b² + c²
aire de l'ellipse : A = π a b
Les droites (MF') et (MF) font le même angle avec la tangente en n'importe quel point de l'ellipse.
e = c / a
Donc e est compris entre 0 et 1
Dans le cadre d'une orbite, on peut dire aussi que :
e = (Ra - Rp) / (Ra + Rp)
où Ra est la hauteur de l'apoapse depuis le centre de la planète
et Rp la hauteur du périapse depuis le centre de la planète.
Le cercle est une ellipse particulière ou :
e = 0
a = b
Les foyers sont confondus
équation cartésienne :
x² / a² + y² / b² = 1
équation paramétrique :
x(t) = a cos t
y(t) = b sin t